The elusive promise of superconductivity, first discovered in 1986, raised hopes that electricity might someday be transmitted with no loss for perfectly efficient power lines and maglev trains, long before energy efficiency top of mind.
Recently researchers at Stanford University and the Department of Energy’s SLAC National Accelerator Laboratory say they have found the first, long-sought proof that the Hubbard model, used to understand electron behavior in numerous quantum materials, can be used to simulate and understand high-temperature superconductivity. This is an important step towards producing and controlling the phenomenon.
The simulations they ran, published in Science, suggest that researchers might be able to toggle superconductivity on and off in copper-based materials called cuprates by tweaking their chemistry so electrons hop from atom to atom in a particular pattern—as if hopping to the atom diagonally across the street rather than to the one next door.
“The big thing you want to know is how to make superconductors operate at higher temperatures and how to make superconductivity more robust,” said study co-author Thomas Devereaux, director of the Stanford Institute for Materials and Energy Sciences (SIMES) at SLAC. “It’s about finding the knobs you can turn to tip the balance in your favor.”
The biggest obstacle to doing that, he said, has been the lack of a model—a mathematical representation of how a system behaves—that describes this type of superconductivity.
While scientists thought the Hubbard model, used for decades to represent electron behavior in numerous materials, might apply to cuprate high-temperature superconductors, until now they had no proof, said Hong-Chen Jiang, a SIMES staff scientist and co-author of the report.
“This has been a major unsolved problem in the field—does the Hubbard model describe high-temperature superconductivity in the cuprates, or is it missing some key ingredient?” he said. “Because there are a number of competing states in these materials, we have to rely on unbiased simulations to answer these questions, but the computational problems are very difficult, and so progress has been slow.”
The many faces of quantum materials
While many materials behave in very predictable ways—copper is always metal, and when you bust up a magnet the bits are still magnetic—high-temperature superconductors are quantum materials, where electrons cooperate to produce unexpected properties. In this case, they pair up to conduct electricity with no resistance or loss at much higher temperatures than established theories of superconductivity can explain.
Unlike everyday materials, quantum materials can host a number of phases, or states of matter, at once, Devereaux said. For instance, a quantum material might be metallic under one set of conditions, but insulating under slightly different conditions. Scientists can tip the balance between phases by tinkering with the material’s chemistry or the way its electrons move around, for instance, and the goal is to do this in a deliberate way to create new materials with useful properties.
One of the most powerful algorithms for modeling situations like this is known as density matrix renormalization group, or DMRG. But because these coexisting phases are so complex, using the DMRG to simulate them requires a lot of computation time and memory and typically takes quite a while, Jiang said.
To reduce the computing time and reach a deeper level of analysis than would have been practical before, Jiang looked for ways to optimize the details of the simulation. “We have to carefully streamline each step,” he said, “making it as efficient as possible and even finding ways to do two separate things at once.” These efficiencies allowed the team to run DMRG simulations of the Hubbard model significantly faster than before, with about a year of computing time at Stanford’s Sherlock computing cluster and other facilities on the SLAC campus.
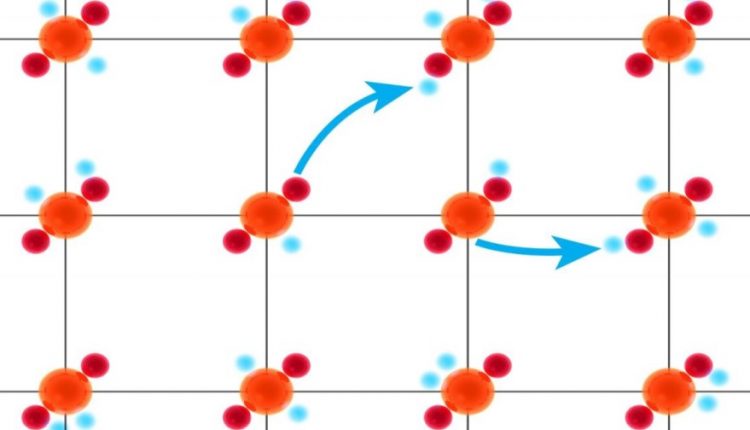
Hopping electron neighbors
This study focused on the delicate interplay between two phases that are known to exist in cuprates—high-temperature superconductivity and charge stripes, which are like a wave pattern of higher and lower electron density in the material. The relationship between these states is not clear, with some studies suggesting that charge stripes promote superconductivity and others suggesting they compete with it.
For their analysis, Jiang and Devereaux created a virtual version of a cuprate on a square lattice, like a wire fence with square holes. The copper and oxygen atoms are confined to planes in the real material, but in the virtual version, they become single, virtual atoms that sit at each of the intersections where wires meet. Each of these virtual atoms can accommodate at most two electrons that are free to jump or hop—either to their immediate neighbors on the square lattice or diagonally across each square.
When the researchers used DMRG to simulate the Hubbard model as applied to this system, they discovered that changes in the electrons’ hopping patterns had a noticeable effect on the relationship between charge stripes and superconductivity.
When electrons hopped only to their immediate neighbors on the square lattice, the pattern of charge stripes got stronger and the superconducting state never appeared. When electrons were allowed to hop diagonally, charge stripes eventually weakened but did not go away, and the superconducting state finally emerged.
“Until now we could not push far enough in our modeling to see if charge stripes and superconductivity can coexist when this material is in its lowest energy state. Now we know they do, at least for systems of this size,” Devereaux said.
It’s still an open question whether the Hubbard model describes all of the incredibly complex behavior of real cuprates, he added. Even a small increase in the complexity of the system would require a huge leap in the power of the algorithm used to model it. “The time it takes to do your simulation goes up exponentially fast with the width of the system you want to study,” Devereaux said. “It’s exponentially more complicated and demanding.”
But with these results, he said, “We now have a fully interacting model that describes high-temperature superconductivity, at least for systems at the sizes we can study, and that’s a big step forward.”
Source: Stanford University